應用奇異擾動理論的突發神經元之數學模型 Mathematics of Bursting Neurons using Singular Perturbation Theory.
多重時間尺度的奇異擾動(singular perturbation)理論的應用在計算神經科學領域越來越受到關注。三位教授Alessio Franci、Guillaume Drion和Rodolphe Sepulchre博士合作發表了一篇關於突發神經元(bursting neurons)的開摺(unfolding)翼狀奇異尖點(winged cusp singularity)的動力學。這篇論文如同其他SIAM的文章充滿了艱澀的數學公式,但在這裡我使用GIF動畫使它易於了解。
目前已知突發神經元(bursting neurons)利用三個不同的時間尺度:在神經脈衝期間快速去極化的快速時間尺度、神經脈衝再極化的慢時間尺度,以及在突發波(burst)期間控制長時間靜止的超慢時間尺度。此篇論文精彩的見解涉及開摺翼狀奇異尖點的電生理學模型。下面所示的GIF動畫顯示了一個簡化的翼狀尖點模型(出自原始論文的圖6和圖7)。本文表明,如果充分分離電生理模型的時間尺度,則可以透過坐標變換得到簡化的正規形式(normal form)。令人驚訝的是,他們表明許多類型的突發神經元可以得到這種簡化的正規形式。根據正規形式的參數,我們可以得到不同種類的突發神經元。
什麼是翼狀尖點(winged cusp)?簡單的來說翼狀尖點是一個看起來像Ω的三次曲線。在GIF動畫上我們可以看到,慢速變量的零斜率線(nullcline)(兩段直線)與快速變量的零斜率線(Ω形狀的曲線)相交於三個位置:左平衡點,中平衡點和右平衡點。左側交叉點位於穩定分支上,因此表示神經元的靜止狀態。中心平衡點位於不穩定的分支處,作為脈衝和休息狀態之間的閾值。右平衡點是表示神經脈衝狀態的不穩定螺線。由於超慢速變量將Ω形向外推,左平衡點消失,只剩下不穩定的脈衝平衡存在。隨著時間的推移,超慢速變量會使Ω形夾緊,從而使系統重新出現左平衡點。在恢復平衡之後,超慢變量鬆弛重新調整Ω形,並再次循環。
另外,聰明的讀者會注意到,當左平衡點消失後且神經元開始產生脈衝,左、中平衡點將重新出現。因為中心平衡點存在,所以脈衝狀態會持續直到Ω形狀收緊產生封閉曲線,使系統回到左平衡點附近的靜止狀態。
-
The use of the theory of singular perturbation of multiple-time scales is gaining traction in the computational neuroscience community. A trio of professors Dr. Alessio Franci, Guillaume Drion, and Rodolphe Sepulchre, have written a paper that relates the dynamics of bursting neurons to the unfolding of a winged cusp singularity. The paper is filled with difficult mathematical formulas, much like any paper from SIAM; however, I find that using a GIF makes it easier to understand.
It has been known for a while that many bursting neurons make use of three separate time scales: the fast time scale for the quick depolarization during a spike, the slow time scale for the repolarization of the spike, and the ultra-slow time scale to control the long periods of quiescence during a burst. The amazing insight of this paper relates electrophysiological models to the unfolding of a winged cusp singularity. Below is a GIF that shows a simplified model of a winged cusp (specifically the model used to generate figures 6 and 7). The paper shows that if an electrophysiological model has sufficient separation of time scales, then it can be reduced via a coordinate transform to this simpler normal form. Amazingly, they show that many kinds of bursters can be reduced to this normal form. Depending on the specifics of the normal form’s parameters, we can get different kinds of bursters.
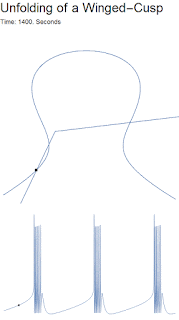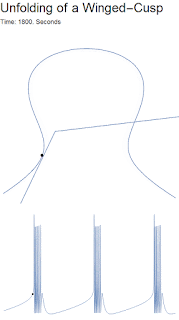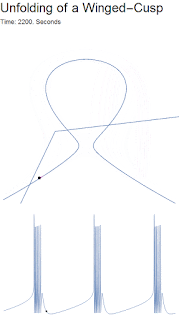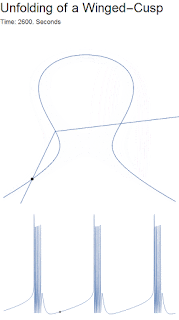
What exactly is a winged cusp? Simply put, it is a cubic curve that looks like an Omega Ω. If we look at the GIF, we see the slow variable's nullcline (the two straight lines) intersects the fast variable's null cline (Omega shaped curve) in three locations: the left equilibrium, the center equilibrium and the right equilibrium. The left equilibrium is the leftmost intersection, and is on the stable branch, and thus represents the neuron at rest. The center is on the unstable branch and acts as a threshold between the spiking and the resting state. The right equilibrium point is an unstable spiral representing the spiking state. As the ultra-slow variable pushes the omega shape outward, the left equilibrium point disappears, and only the unstable spiking equilibrium exists. Over time the ultra-slow causes the Omega to pinch off, thus allowing the system to return to the left equilibrium. After returning to equilibrium the ultra-slow variable relaxes, reforming the Omega, and allowing the cycle to begin again.
Note, an astute reader will notice that after the left equilibrium has disappeared and the neuron begins spiking the left and center equilibrium will reappear. Because the center equilibrium now exists, the spiking state does not stop until the Omega forms a close loop, allowing the system to return to rest near the left equilibrium.
-
原始論文:
Franci, Alessio, Guillaume Drion, and Rodolphe Sepulchre. "Modeling the modulation of neuronal bursting: a singularity theory approach." SIAM Journal on Applied Dynamical Systems 13.2 (2014): 798-829.
http://epubs.siam.org/doi/abs/10.1137/13092263X
-
It has been known for a while that many bursting neurons make use of three separate time scales: the fast time scale for the quick depolarization during a spike, the slow time scale for the repolarization of the spike, and the ultra-slow time scale to control the long periods of quiescence during a burst. The amazing insight of this paper relates electrophysiological models to the unfolding of a winged cusp singularity. Below is a GIF that shows a simplified model of a winged cusp (specifically the model used to generate figures 6 and 7). The paper shows that if an electrophysiological model has sufficient separation of time scales, then it can be reduced via a coordinate transform to this simpler normal form. Amazingly, they show that many kinds of bursters can be reduced to this normal form. Depending on the specifics of the normal form’s parameters, we can get different kinds of bursters.
What exactly is a winged cusp? Simply put, it is a cubic curve that looks like an Omega Ω. If we look at the GIF, we see the slow variable's nullcline (the two straight lines) intersects the fast variable's null cline (Omega shaped curve) in three locations: the left equilibrium, the center equilibrium and the right equilibrium. The left equilibrium is the leftmost intersection, and is on the stable branch, and thus represents the neuron at rest. The center is on the unstable branch and acts as a threshold between the spiking and the resting state. The right equilibrium point is an unstable spiral representing the spiking state. As the ultra-slow variable pushes the omega shape outward, the left equilibrium point disappears, and only the unstable spiking equilibrium exists. Over time the ultra-slow causes the Omega to pinch off, thus allowing the system to return to the left equilibrium. After returning to equilibrium the ultra-slow variable relaxes, reforming the Omega, and allowing the cycle to begin again.
Note, an astute reader will notice that after the left equilibrium has disappeared and the neuron begins spiking the left and center equilibrium will reappear. Because the center equilibrium now exists, the spiking state does not stop until the Omega forms a close loop, allowing the system to return to rest near the left equilibrium.
-
原始論文:
Franci, Alessio, Guillaume Drion, and Rodolphe Sepulchre. "Modeling the modulation of neuronal bursting: a singularity theory approach." SIAM Journal on Applied Dynamical Systems 13.2 (2014): 798-829.
http://epubs.siam.org/doi/abs/10.1137/13092263X
-
撰稿:Alexander White
翻譯:高暐哲


留言
張貼留言