雙神經元的耦合與震盪

https://mire-growth-131.notion.site/c1ada3de3ae542d8bcad819f26619382

循環神經網路(Recurrent Neural Network, RNN)是人工神經網路(Artifical Neural Network, ANN)的一種分之。RNN在自然語言處理(NPL)、手寫辨識和語音識別都有很好的應用。可以透過分岔流形(bifurcation manifold) 去了解RNN複雜的動力學行為。Steil, Jochen Jakob分析雙神經元的全連結網路，將外部對神經元的刺激視為分叉參數(bifurcation parameters)，找到網路穩定震盪的區域。

網路模型

$$ \left\{\begin{array}{l}s_1=\sigma\left(\omega_{11}s_1+\omega_{12}s_2+u_1\right)\\s_2=\sigma\left(\omega_{21}s_1+\omega_{22}s_2+u_2\right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1)\end{array}\right.\\\left\{\begin{array}{l}\sigma_{\tan h}(x)=\tan h(x)\\\sigma_{fermi}(x)=\frac1{1+e^{-x}}=\frac12\left(\tan h\left(\frac x2\right)+1\right)\;\;\;\;\;\;\;\;\;(2)\end{array}\right.\\\\ $$

公式(1)，s1和s2表示穩定的神經激發頻率。Wij表示神經j到神經i的連結強度。ui表示外界給神經i的刺激。公式(2)，$\sigma$表示激活函數(activation function)，兩種常見的函數有 tanh 和 fermi。

分岔曲線(bifurcation curve)

$$ \overline h=W\overline S+U=\begin{pmatrix}\omega_{11}{\overline s}_1+\omega_{12}{\overline s}_2+u_1\\\omega_{21}{\overline s}_1+\omega_{22}{\overline s}_2+u_2\end{pmatrix}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(3)\\D=\delta_{ij}\sigma'(h)=\begin{pmatrix}\sigma'({\overline h}_1)&0\\0&\sigma'({\overline h}_2)\end{pmatrix}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(4)\\J=J(\overline s)=D(\overline s)W=\begin{pmatrix}\omega_{11}\sigma'({\overline h}_1)&\omega_{12}\sigma'({\overline h}_1)\\\omega_{21}\sigma'({\overline h}_2)&\omega_{22}\sigma'({\overline h}_2)\end{pmatrix}\;\;\;\;\;\;\;\;\;\;(5)\\\\ $$

公式(3)，h表示神經處於穩定狀態時激活函數的輸入。公式(4)，D為對角化矩陣，對角的值為h放進激活函數的微分 $\sigma'$。公式(5)，J為Jacobian，D與連接矩陣W相乘，可以將J的特徵值分三種結果討論(圖1)

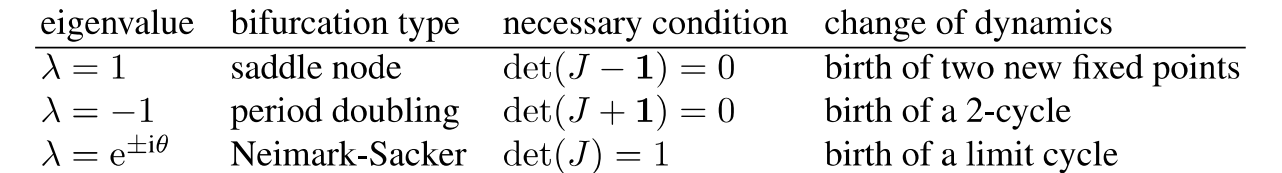圖1，三種特徵值

$$\textstyle{\overline s}_i=\sigma(\sum_{}\omega_{ij}{\overline s}_j+u_i)\Leftrightarrow u_i=\sigma^{-1}({\overline s}_i)-\sum_{}\omega_{ij}{\overline s}_j\;\;\;\;\;\;\;\;\;\;\;\;\;(6)\\\left\{\begin{array}{l}\sigma'_{\tan h}\left({\overline h}_i\right)=1-\sigma_{\tan h}^2\left({\overline h}_i\right)=1-{\overline s}_i^2\\\sigma'_{fermi}\left({\overline h}_i\right)=\sigma_{fermi}\left({\overline h}_i\right)\left(1-\sigma_{fermi}\left({\overline h}_i\right)\right)={\overline s}_i\left(1-{\overline s}_i\right)\;\;\;\;\;(7)\end{array}\right.$$

公式(6)，為神經平衡狀態的等校公式。公式(7)，激活函數的微分。接著將公式(6)(7)代入圖(1)的三種條件可以將s1和s2分開。下面以tanh function 的Neimark-Sacker為例。(圖2)為全部整理的結果。
$$\begin{array}{l}以\;\tanh\;function\;的\;Neimark-Sacker\;\mathrm{為例}\\det(J)=\omega_{11}\sigma'({\overline h}_1)\omega_{22}\sigma'({\overline h}_2)\;-\;\omega_{12}\sigma'({\overline h}_1)\omega_{21}\sigma'({\overline h}_2)=det(W)\sigma'({\overline h}_1)\sigma'({\overline h}_2)\;=1\\\Rightarrow1=det(W)\sigma'({\overline h}_1)\sigma'({\overline h}_2)\;=det(W)\left(1-{\overline s}_1^2\right)\left(1-{\overline s}_2^2\right)\\\Rightarrow{\overline s}_2=\pm\sqrt{1-\frac1{det(W)\left(1-{\overline s}_1^2\right)}}\end{array}$$

圖2，兩種激活函數在三種特徵值的整理結果

與神經連結無關的動態系統

圖3是在特定連結強度下兩種激活函數的分岔曲線。可根據外界的刺激, u1和u2,判斷會形成的狀態。區域1，只形成一個不動點 (fixed point)。區域2，包含三個不動點，兩個穩定+一個不穩定。區域3，包含複雜的動力學，包含鎖頻 (frequency locking)。區域4，雙週期震盪。

圖3，兩種激活函數的分岔曲線

總結

將神經激發頻率(s1, s2)轉換成外界刺激u1和u2。將u1和u2當作當作分岔參數，觀察不同刺激輸入網路時震盪的狀況，包單固定點、三固定點、含鎖頻和雙周期。

撰文：謝明儒

參考資料

1.  Haschke, R., Steil, J. J., & Ritter, H. (2001, August). Controlling oscillatory behaviour of a two neuron recurrent neural network using inputs. In International Conference on Artificial Neural Networks (pp. 1109-1114). Springer, Berlin, Heidelberg.

2. Haschke, R., & Steil, J. J. (2005). Input space bifurcation manifolds of recurrent neural networks. Neurocomputing, 64, 25-38.

3. Kuznetsov, Y. A., Kuznetsov, I. A., & Kuznetsov, Y. (1998). Elements of applied bifurcation theory

 (Vol. 112, pp. xx+-591). New York: Springer.