Hopf Bifurcation

A Hopf bifurcation is a canonical bifurcation that gives rise to limit cycles. We previously discussed the Saddle node on the invariant circle. The Hopf bifurcation is a different mechanism that gives rise to a limit cycle. Here the limit cycle emerges from the equilibrium point. It is intimately related to the eigenvalues associated around a fix point. It is related to resonance. 

A Hopf bifurcation occurs when an equilibrium point of a two-dimensional (or higher) non-linear dynamic system has a pair of complex conjugate eigenvalues change from negative real part to positive real part. 

This is a mouthful of a definition, so let's use a canonical example of a Hopf bifurcation.

$$\frac{dx}{dt}= + a x - \omega y - x(x^2 + y^2)$$

$$\frac{dy}{dt} = \omega x + a y - y(x^2+y^2)$$

Here $a$ is the bifurcation parameter, we will show that $a$ is the square of the radius. $\omega$ is the frequency of the limit cycle. In figure 1 you can see that when $a\leq$0 there is only a single fixed point. When $a > 0$ there is a sudden change in the dynamics; there is now a stable limit cycle. 

 

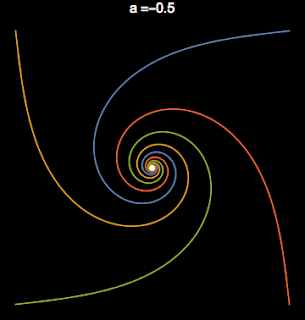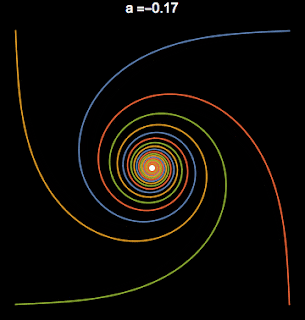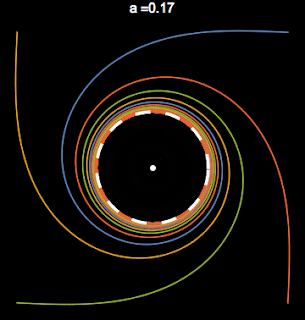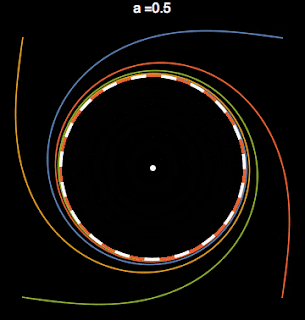A Supercritical Hopf Bifurcation sweeping through the parameter $a$. When $a>0$ there is a limit cycle.

 

To see why this is the case, let's convert everything into polar coordinates. By setting $x = r \cos(\theta)$ and $y = r \sin(\theta)$ we get 

$$-\frac{d\theta}{dt} r \sin(\theta) + \frac{d r}{dt} \cos(\theta)= + a r \cos(\theta) - \omega r \sin(\theta) - r^3 \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta))$$

$$\frac{d\theta}{dt} r \cos(\theta) + \frac{d r}{dt} \sin(\theta) = \omega r \cos(\theta) + a r \sin(\theta) -r^3 \sin(\theta)(\cos^2(\theta)+\sin^2(\theta))$$

We can solve for the change in radius $\frac{dr}{dt}$

$$\frac{-\frac{d\theta}{dt} r \sin(\theta) + \frac{d r}{dt} \cos(\theta)}{ r\sin(\theta)}=\frac{ + a r \cos(\theta) - \omega r \sin(\theta) - r^3 \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta)) }{ r\sin(\theta)}$$

$$- \frac{d\theta}{dt}+  \frac{  \frac{d r}{dt} \cos(\theta)}{ r\sin(\theta)}=\frac{ + a r \cos(\theta) - \omega r \sin(\theta) - r^3 \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta)) }{ r\sin(\theta)}$$

and

$$\frac{\frac{d\theta}{dt} r \cos(\theta) + \frac{d r}{dt} \sin(\theta)}{ r \cos(\theta)} = \frac{\omega r \cos(\theta) + a r \sin(\theta) -r^3 \sin(\theta)(\cos^2(\theta)+\sin^2(\theta)) }{ r \cos(\theta)}$$

$$\frac{d\theta}{dt} + \frac{ \frac{d r}{dt} \sin(\theta)}{ r \cos(\theta)} = \frac{\omega r \cos(\theta) + a r \sin(\theta) -r^3 \sin(\theta)(\cos^2(\theta)+\sin^2(\theta)) }{ r \cos(\theta)}$$

Add the equations together 

$$\frac{ \frac{d r}{dt} \sin(\theta)}{ r \cos(\theta)}+  \frac{  \frac{d r}{dt} \cos(\theta)}{ r\sin(\theta)} = \frac{\omega r \cos(\theta) + a r \sin(\theta) -r^3 \sin(\theta)(\cos^2(\theta)+\sin^2(\theta)) }{ r \cos(\theta)}+\frac{ + a r \cos(\theta) - \omega r \sin(\theta) - r^3 \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta)) }{ r\sin(\theta)}$$

Simplify fractions

$$\frac{ \frac{d r}{dt} \sin^2(\theta)+   \frac{d r}{dt} \cos^2(\theta)}{ r\sin(\theta)\cos(\theta) }= \frac{\omega r \cos(\theta) \sin(\theta) + a r \sin^2(\theta) -r^3 \sin^2(\theta)(\cos^2(\theta)+\sin^2(\theta))  + a r \cos^2(\theta) - \omega r\cos(\theta) \sin(\theta) - r^3 \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta)) }{ r\sin(\theta)\cos(\theta)}$$

More Simplifying (recall $\sin^2 +\cos^2 =1$)

$$\frac{d r}{dt} =  + a r(\cos^2(\theta)+ \sin^2(\theta) )-r^3(\cos^2(\theta)+ \sin^2(\theta) )(\cos^2(\theta)+ \sin^2(\theta) )$$

$$\frac{dr}{dt} = a r -r^3$$

We can do the same trick with the change in phase $\frac{d\theta}{dt}$ 

$$\frac{-\frac{d\theta}{dt} r \sin(\theta) + \frac{d r}{dt} \cos(\theta)}{ \cos(\theta)}=\frac{ + a r \cos(\theta) - \omega r \sin(\theta) - r^3 \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta)) }{ \cos(\theta)}$$

$$\frac{dr}{dt}-  \frac{  \frac{d \theta}{dt} r \sin(\theta)}{ \cos(\theta)}=\frac{ + a r \cos(\theta) - \omega r \sin(\theta) - r^3 \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta)) }{ \cos(\theta)}$$

and

$$\frac{\frac{d\theta}{dt} r \cos(\theta) + \frac{d r}{dt} \sin(\theta)}{ \sin(\theta)} = \frac{\omega r \cos(\theta) + a r \sin(\theta) -r^3 \sin(\theta)(\cos^2(\theta)+\sin^2(\theta)) }{ \sin(\theta)}$$

$$\frac{dr}{dt} + \frac{ \frac{d \theta}{dt} r \cos(\theta)}{  \sin(\theta)} = \frac{\omega r \cos(\theta) + a r \sin(\theta) -r^3 \sin(\theta)(\cos^2(\theta)+\sin^2(\theta)) }{ \sin(\theta)}$$

Subtract the equations to get

$$\frac{ \frac{d \theta}{dt} r \cos(\theta)}{  \sin(\theta)} +  \frac{  \frac{d \theta}{dt} r \sin(\theta)}{ \cos(\theta)}= \frac{\omega r \cos(\theta) + a r \sin(\theta) -r^3 \sin(\theta)(\cos^2(\theta)+\sin^2(\theta)) }{ \sin(\theta)}- \frac{ + a r \cos(\theta) - \omega r \sin(\theta) - r^3 \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta)) }{ \cos(\theta)}$$

Simplify fractions to get 

$$\frac{ \frac{d \theta}{dt} r \cos^2(\theta)+    \frac{d \theta}{dt} r \sin^2 (\theta)}{ \sin(\theta) \cos(\theta)}= \frac{\omega r \cos^2(\theta)+ a r \sin(\theta) \cos(\theta) -r^3 \cos(\theta) \sin(\theta)(\cos^2(\theta)+\sin^2(\theta)) - a r \sin(\theta) \cos(\theta) + \omega r \sin^2 (\theta) + r^3 \sin(\theta) \cos(\theta)(\cos^2(\theta)+ \sin^2(\theta)) }{ \cos(\theta)\sin(\theta)}$$

Cancel everything to get 

$$\frac{d \theta}{dt} r \cos^2(\theta)+    \frac{d \theta}{dt} r \sin^2 (\theta) =  \omega r (\cos^2(\theta)+ \sin^2(\theta))$$

$$\frac{d\theta}{dt} r = \omega r$$

$$\frac{d\theta}{dt}  = \omega$$

This gives us a differential equation expressed in polar coordinates

$$\frac{dr}{dt} = a r -r^3$$

$$\frac{d\theta}{dt} = \omega$$

Solving for the steady state for $r$ yields $r=0$ the equilibrium or $r =\sqrt{a}$ is the limit cycle. $\theta =\omega t$ is just  the frequency of the limit cycle. Now we can see why only $a>0$ allows limit cycles, as $0 = a r- r^3$ has more than one root when $a >0$. 

Now that we have some intuition for the bifurcation parameter $a$ we can next analyze when this occurs. As I said, it's when a pair of complex conjugate eigenvalues cross the imaginary axis. 

Let's begin by calculating the Jacobian matrix of the canonical system

$$\begin{bmatrix} a & -\omega \\ \omega & a \\ \end{bmatrix}$$

This matrix has eigenvalues $$\lambda = a \pm i \omega$$

Thus we can see that when $a < 0$ the fixed point is stable and there is no limit cycle. $a = 0$ has two purely imaginary eigenvalues. There is no limit cycle because the non-linear terms stabilize the fixed point. However, when $a >0$ the limit cycle appears. 

It is important to note, we have been discussing the supercritical Hopf bifurcation. This is the case when a stable equilibrium point bifurcates into a stable limit cycle and a unstable equilibrium point. A subcritical Hopf bifurcation has canonical form 

$$\frac{dx}{dt}= + a x - \omega y + x(x^2 + y^2)$$

$$\frac{dy}{dt} = \omega x + a y + y(x^2+y^2)$$

or 

$$\frac{dr}{dt} = -a r + r^3$$

$$\frac{d\theta}{dt} = \omega$$

Here, this is when an unstable equilibrium point bifurcates into a stable equilibrium and an unstable equilibrium. 

When $a$ is sufficiently small, the Hopf bifurcation will occur (and give rise to a limit cycle) when the non-linear terms are highly complicated. Depending on the non-linear terms, the frequency won't be $\omega$, and the shape won't be a circle. If $a$ becomes very large, the system may undergo other bifurcations, but this gives a great intro to the Hopf bifurcation.

Author: Alexander J. White