當神經網路遇上科學
https://pikapei.notion.site/a30390aad8cd438baacb86941c94a43b
深度學習因為強大的學習力,被廣泛研究並運用於各個領域,也斬獲了相當出色的成果。但訓練的過程通常需要大量的資料,若資料量不足,常藉由合成資料、半監督式學習或自監督式學習等架構來彌補,否則深度學習就無法發揮作用。
但如果,我們可以把已知的事物加入訓練模型中,就可以對模型加以限制,並且用比較少的資料完成訓練。有許多的框架都在追求這樣的目標,例如近年來熱門的physics-informed neural network[1],即是以偏微分方程解作為懲罰項(penalty)加入損失函數(loss function)。而今天介紹的這篇論文,則是把已知資訊直接寫入微分方程,把未知的部分以神經網路代入來擬合資料,作者將此稱為通用微分方程(universal differential equation, UDE)。
神經常微分方程 (Neural Ordinary Differential Equations)
在介紹通用微分方程前,先了解最核心的概念來自於神經常微分方程這篇研究[2],透過一個神經網路表示未知的微分方程,如下面式子(NN表示Neural Network、θ代表神經網路的參數):
$$\dot{u} = \text{NN}_θ (u, t)$$
舉例來說,假如我們有一筆指數成長的時間序列資料(假設微分方程為:$\dot{x}=2x$),但我們不知道怎麼列出式子,就可以建立一個神經網路$\dot{x}=\text{NN}_\theta(u,t)$,訓練他去擬合我們有的資料,再進行預測。神經常微分方程的概念,讓一般認為一層一層離散的神經網路連續化,更適合運用在時間間隔沒有一定規律的資料集。
通用微分方程
和前段以神經網路來代表整個微分方程不同,通用微分方程的架構則是把已知部分直接列進方程式,未知部分再以神經網路取代,舉論文中的一個例子 Lotka-Volterra 模型,這個模型描述了狩獵者和獵物之間此消彼長的數量變化,方程式如下(x代表兔子數量、y代表狼的數量):
$$\dot{x} = αx − βxy$$
$$\dot{y} = γxy − δy$$
對照圖一,我們可以看到,x(兔子)會因為自身繁衍指數增加、被狼捕食而減少;y(狼)因為有兔子吃而增加、族群互相競爭而減少。
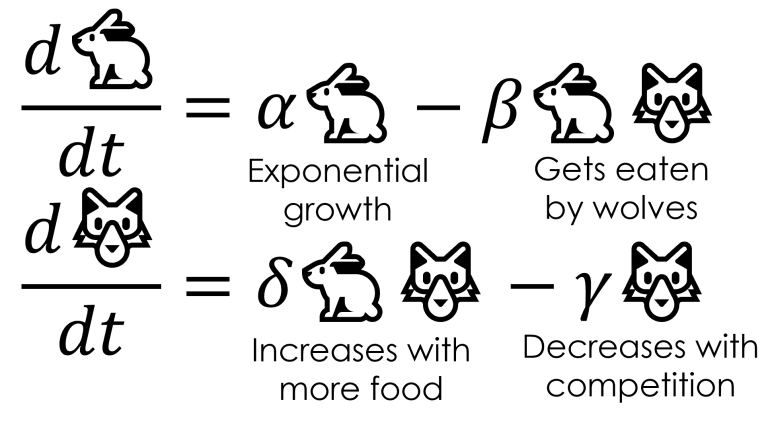 |
| 圖一,來源:參考資料[3] |
如果現在,假設我們知道兔子會繁衍指數增加和其增長率α,可以列出$\dot{x}=αx$;知道狼群競爭會指數減少但不知道衰減率,列出$\dot{y}=−θ_1y$,最後兔子、狼之間的交互關係為未知,代以神經網路後,我們可以列出下列方程式:
$$\dot{x}=αx + U_1(θ,x,y)$$
$$\dot{y}= −θ_1y + U_2(θ,x,y)$$
其中神經網路$U_1$、$U_2$和未知參數$\theta_1$都可以從訓練得到。觀看圖二,t≤6之前是訓練資料,將訓練好的模型拿來做時間序列預測,可以看到模型確實學到震盪的動力學行為並展示出頗為精確的預測。
 |
| 圖二 |
結語
微分方程是各個科學領域中用來描述世界的語言,透過將我們已知的背景知識加上強大的神經網路,通用微分方程除了可以用較少的資料來訓練模型之外,也增加了鑲嵌其中神經網路的可解釋性(interpretability)。目前在Julia程式語言中的DiffEqFlux.jl套件[4](原始論文第一作者即是套件主要開發者)已經相當完整,有興趣的讀者可以前往試試看!
撰稿:黃宣霈 H. P. Huang
原始論文:
Rackauckas, C., Ma, Y., Martensen, J., Warner, C., Zubov, K., Supekar, R., ... & Edelman, A. (2020). Universal differential equations for scientific machine learning. arXiv preprint arXiv:2001.04385.
參考資料:
1. Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics, 378, 686-707.
2. Chen, R. T., Rubanova, Y., Bettencourt, J., & Duvenaud, D. K. (2018). Neural ordinary differential equations. Advances in neural information processing systems, 31.


留言
張貼留言