具有動態反應控制的自調節神經網路 PID

本研究提出了一種基於反向傳播人工神經網絡（ANN）的自適應PID（比例積分微分）控制器，如圖一，用於直流電機的速度控制。傳統的PID控制器需要調整其增益以適應不同條件下的系統反應。而這項研究的自適應PID控制器根據期望的輸出使用ANN計算適當的增益。而期望的輸出，即系統階躍反應（step response）的暫態部分和穩態部分的動態反應。該方法的創新之處在於除了使用誤差進行網絡訓練外，還使用了最大超調（overshoot）、穩定時間（settling time）和靜態誤差的期望值作為網絡的輸入數據。

研究首先使用遺傳演算法（genetic algorithm）建立了一個離線訓練數據庫，其中包含與PID增益相關的動態反應數據。這個數據庫用於ANN的訓練。接著，ANN根據誤差和期望反應估算適當的增益組合，以適應系統的誤差和期望反應。

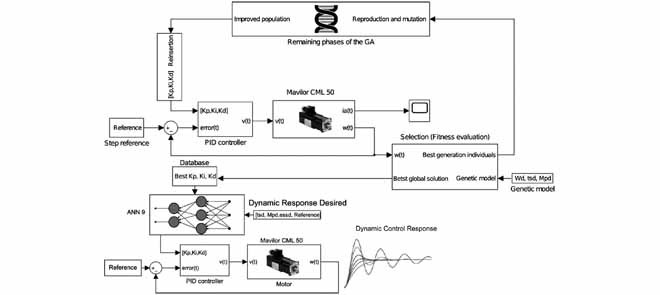圖一、整體架構圖

圖二、簡寫代表意思

第I部分

    本研究提出一種基於人工神經網絡（ANNs）的PID自調系統，用於控制直流馬達的轉速。與目前的調參研究不同，選擇反映過渡階段和穩態的3個參數，本研究選擇所需的動態反應。使用基於遺傳演算法（GA）獲得的數據庫對反向傳播ANN進行訓練以實現這一目標。GA確保在可能的操作條件下分佈數據，並拒絕使系統振蕩或不穩定的增益組合。

    ANN的輸入為馬達的輸出和步階參考（step reference）。表示動態反應的輸入向量為[Mp；ts；ess；參考]。另一方面，輸出向量被視為[Kp Ki Kd]。這些向量允許ANN自我調整增益，以在各種操作條件和參考下控制直流馬達。

    系統的動態反應可能因分析的系統和使用的控制信號而異。本文的目的是獲得一種自調程式，使得可以選擇所需的反應，因為根據應用，可能需要不同的動態反應。圖三（b）顯示了根據所選K的組合，PID控制器可能具有的可能輸出。一種有用的組合會生成無振蕩但帶有超調的反應。這種類型的反應在需要速度且精度不是關鍵因素時是有用的。一個例子是使用無人機進行監視，其中需要車輛快速移動並且超調不會對任務產生重大影響。另一方面，還可以獲得慢但精確的反應，由於系統需要更長的時間才能達到參考，但不會有超調。例如，焊接或切割機器人不能超越參考，因為在這些應用中，超調意味著任務崩潰或嚴重故障。綜上所述，本文提出的系統被呈現為一種自調選擇，適應應用所需的反應，並根據用戶或應用的需求使其更快或更慢。

圖三、動態反應

第II部分 基於遺傳演算法的資料庫

    遺傳演算法（GA）受基因選擇方式的啟發。GA的目標是離線構建一個將PID增益與其動態反應相關聯的資料庫。通過這種方式，該演算法尋找能夠獲得特定期望動態反應的增益。本研究採用了一種固定狀態的GA，其中演算法從一個隨機種群開始，其中每個個體都是一個包含三個PID增益（Kp，Ki和Kd）的向量，考慮到PID控制的規律由（1）式描述。

$$U(t)=K_{p}e(t)+K_{i}\int e(t)dt+K_{d}\frac{\mathrm{d} e(t)}{\mathrm{d} t}\cdot \cdot \cdot \cdot \cdot \cdot (1)$$

    演算法的第一步是隨機創建個體。隨後，評估每個個體的適應度，以選擇適應性更好的個體。適應度通過歐幾裡得距離來評估，如（2）所示：

$$f=\sqrt{(ts_{d}-ts)^2+(M_{pd}-M_p)^2+(ess_d-ess)^2}\cdot \cdot \cdot \cdot \cdot \cdot (2)$$

其中，f是適應度值，下標d表示期望值。考慮到期望值是系統反應中預期的最大值。因此，如果實際值小於期望值，那麼該變數對f值的貢獻將為零。之後，進入其他GA階段，包括繁殖、變異和將後代與原始倖存種群混合。圖四描述了整個過程。

圖四、遺傳演算法（GA）

    本研究中使用的植物是Mavilor品牌的DC電機型號CML-050。一旦定義了被控物和演算法所需的參數，GA就會反覆運算運行。該過程顯示在圖五中。這個過程通過遺傳模型（GM）的隨機值重複，以評估具有不同tsd、Mpd、essd和參考組合的情況。隨後，保存滿足GM要求的增益在資料庫中，將用於神經網路訓練的資料庫中。總共類比了10296種不同GM的組合來構建資料庫。這些值被選擇以保持反應在電機的操作極限範圍內。所使用的資料庫具有包含ts、Mp、ess、reference、Kp、Ki和Kd的向量。這個演算法的幾個結果可以在圖六中以圖形方式看到，在表一中以數位元元元方式看到。

圖五、基於遺傳演算法的資料庫

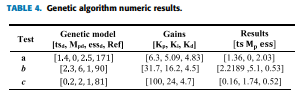表一、GA結果

圖六、GA結果

第III部分 人工神經網路作為自調節器

    在這一部分，開發了一個反向傳播人工神經網路（ANN）。ANN使用前一部分獲得的資料庫進行訓練。資料庫被分為輸入（ts、Mp、ess、Ref）和輸出（Kp、Ki、Kd），以便與ANN一起工作。

    在ANN的第一階段，需要選擇架構的適當參數。在這項工作中，初始架構基於幾何金字塔法則。隨後，根據網路性能調整了架構。進行了多次類比以測試不同架構的性能，以RMSE作為性能度量。這些測試的最相關結果可以在表二中看到。

表二、ANN不同架構的效能

    從表二中可以看到，體系結構9是提供最佳輸出的網路，具有較低的RMSE。該誤差是每個增益（Kp，Ki，Kd）的平均RMSE。因此，選擇使用這種體系結構。

    在圖七中，可以看到提議的自調整器的一般過程。網路需要GM的所有四個參數，之後網路將計算出三個適當的增益。隨後，PID可以獲得期望的動態反應。Matlab-Simulink環境用於執行模擬。Matlab運行GM，而Simulink負責模擬PID、ANN和電機動力學。

圖七、人工神經網路作為自調節器

第IV部分 結果

    本節展示了ANN作為調諧代理的結果。測試資料集的結果在RMSE方面為14.83%。為了評估ANN在動態反應中的性能，提出了十個隨機的GM組合。這些值的組合之前沒有在任何資料集中使用過。所選值顯示在表三中。表四中呈現的結果是使用表三中的GM得到的結果。GM代表使用者可能根據所需的應用所需的不同操作條件。

表三、遺傳模型（網路輸入）

表四、網路結果（網路輸出 數值）

圖八、網路結果（網路輸出 階躍反應）

    圖八說明瞭所提出的GA的階躍反應。可以觀察到ANN估計的Kp，Ki和Kd的動態反應。圖像允許監視特定情況下的性能，從動態反應的角度評估整體網路性能。表五顯示了每個輸入變數的誤差。

表五、變數誤差

    此外，進行了測試以觀察在其他參數保持不變的情況下輸入參數的變化。通過參數變化，使用ANN計算了進一步的增益，並分析了系統給定的階躍反應。這些測試使用了表三表四中的GM9，該表在特定模型的研究中表現最差。首先變化的是tsd。

圖九、一個輸入參數變化的誤差變化

    圖九a顯示了在tsd的值變化時，其他輸入的誤差變化（期望值-實際值）。圖8b說明瞭當Mpd的值變化時誤差的變化。圖8c顯示了當essd的百分比變化時誤差的變化。儘管存在變化，上述圖像表明網路性能隨著輸入參數工作範圍的變化而變化。

    使用用於測試所提出的自調節器性能的測試資料集獲得的結果表明，86%的資料（1327個組合）符合所需的要求或更低的值，即：ts <tsd，ess <essd和Mp <Mpd。此外，所有測試資料都顯示提供穩定反應。結果表明在操作範圍內具有穩定的反應，可接受的誤差降低性能，最重要的是對動態反應的控制，這是該工作的主要目標。

第V部分 結論

    本文提出了一種使用人工神經網路的自調節系統，可以控制直流電機的速度以及期望的反應類型。與其他使用人工神經網路的自調節研究不同，在這項工作中，使用了通過遺傳演算法構建的資料庫。遺傳演算法確保網路的訓練資料不包括會引起振盪的增益組合，並使我們能夠選擇所需的動態反應。

    這項研究的一個缺點是網路的性能與系統的操作範圍相關聯，如圖九所示。這意味著儘管雖然可以控制系統的反應，但精度不會保持恒定，並且在系統操作極限下性能下降。另一個限制是一些組合是在物理上不可能實現的系統。但是，所提出的方法沒有考慮識別這些組合的任何方式。

撰文：陳祖喬

References:

O. Rodríguez-Abreo, J. Rodríguez-Reséndiz, C. Fuentes-Silva, R. Hernández-Alvarado and M. D. C. P. T. Falcón, "Self-Tuning Neural Network PID With Dynamic Response Control," in IEEE Access, vol. 9, pp. 65206-65215, 2021, doi: 10.1109/ACCESS.2021.3075452.