具視覺層級的神經網路：等變群局部稀疏編碼

人類大腦對於如何從感官去建立一個模型來表達周遭環境，甚至進行推理、學習、預測等等，一直有一套獨特的方法。從貝氏統計的角度來看，我們應能從先驗知識與機率分佈來對未知數進行推論。因此，問題就成了：如何產生一個能推論因果關係的呈現方式，並能與感官傳來的訊息互相「轉譯」。以視覺為例，我們能用變換群如旋轉、平移、縮放、亮度變化等來表示整張或者圖片的一部分如何隨著時間變換。除此之外，視覺也有所謂層級的概念：我們先看到整個場景，後看到個別物體，每個物體都有自己的姿態，最後還能再解構成更小的視覺特徵。這種層級若能與變換群相容，我們就擁有了一個與大腦相似的呈現方式。在近期，稀疏編碼被用來進行此種呈現：它使用一組圖像特徵來組成一本「字典」，而各種圖片都可以藉由字典中的特徵排列組合出來。利用循環動態來表達這些圖像特徵，我們就能夠建立一套機器學習架構，包含能量函數、用於最小化此函數的局部競爭算法(Locally Competitive Algorithm, LCA)、以及向後傳播來進行字典本身的學習。

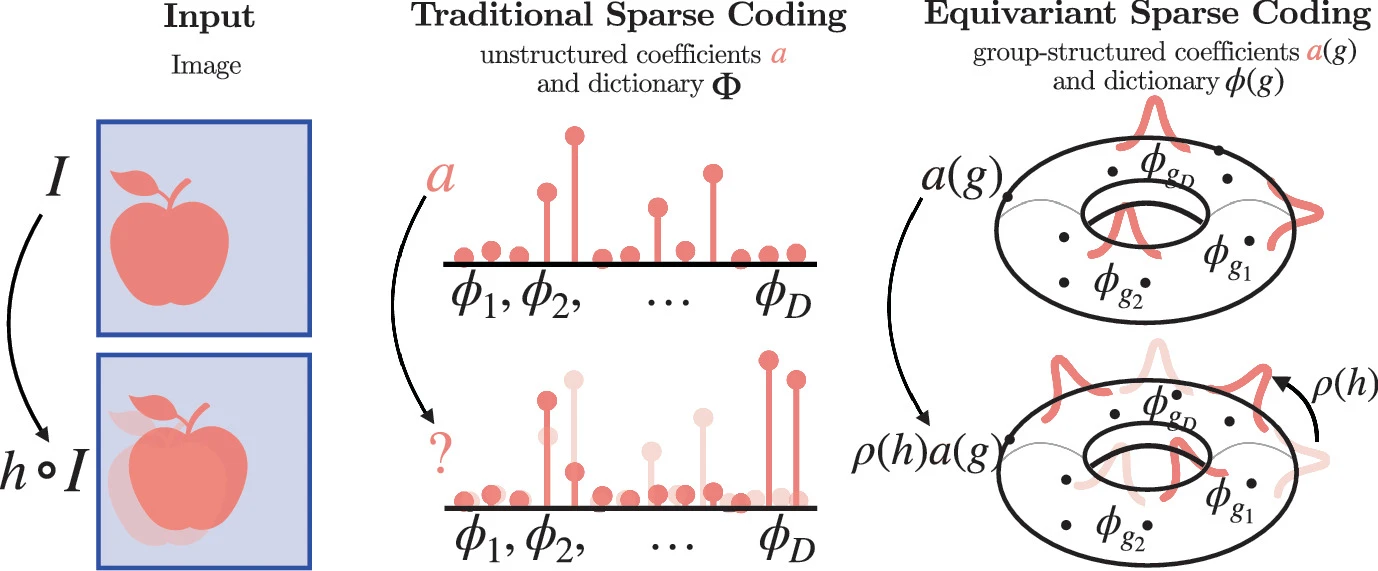圖一：傳統與等變稀疏編碼對圖片I進行編碼，並被群作用h變換前後的幾何呈現。這個甜甜圈代表了所有可能的變換(如各種角度的旋轉、平移等)，而上面的尖刺代表實際作用在圖片的變換分佈。新方法的好處是能擁有更具規範、可預測的編碼方式。

先前的研究已透過機器學習的方式或手動進行關聯，探索了稀疏編碼字典中各特徵之間的關係。近期幾何深度學習 (Goemetric Deep Learning, GDL) 進一步藉由分組(群)卷積將群的等變性引入(註一)。但它們前饋及缺少層級推論的特性，使得我們無法建立場景的局部-全局關係。UCB 的研究人員為此提出了具備「群等變性」的層級結構(Shewmake, Miolane, and Olshausen 2023)，並將其應用到稀疏編碼之上。透過定義良好的群作用、字典特徵的格式，我們可以藉由新的LCA動態、分組卷積構成的局部連接、能量函數等等，來建構一個同時相容等變性以及層級推論的生成模型。這個模型的功效在一合成的資料集被檢驗。此資料集使用低級特徵為基本單元，透過各種變換組合成為不同的高級特徵。如附圖，此資料集展示了所提出模型的分層結構及其稀疏與等變性，並最終能生成與原圖一致的結果。

圖二：（左）生成模型。此模型直觀地將字典中各個特徵 “a” 線性地加總，並得到一張完整的圖片。（中）能量函數與LCA動態。能量函數包含了實際圖片與生成模型輸出的差、字典特徵的稀疏性，LCA動態則由Leaky term、同層其他神經的權重、與對應特徵的相似度組成。（右）LCA網路。

圖三：（左）幾何生成模型。（右）李群作用關聯字典的各特徵。

圖四：（左）一個具有兩層的平移等變架構，其內部和層間都有循環連接。（右）實驗結果，展示神經動態收斂到一個稀疏的、層級的場景表示；該表示隨著輸入影片的時間等變地變換。第1列：輸入的各個影片幀，第2列：顯示稀疏等變激勵的第一層Gabor係數映射。第3和4列：顯示稀疏等變激勵的兩個第二層「物體」係數映射。（註二）

透過引入群論的概念及其結構，研究人員提出了在面對各種圖片變換時仍能維持一致性推論的稀疏編碼模型。此種一致性不只針對整張圖片，同時也利用了多層神經來達成局部及局部-全局的一致，正如同我們的大腦視覺皮質。此模型因此可能可以讓我們更了解諸如物件辨識、姿態估計、深度估計等等，是怎麼在大腦中達成的。也因其網路連接的局部性及對稱性，使得GPU可以簡單地對其實現平行化，對未來在神經科學及人工智慧的探索上都有所貢獻。

註一：舉例來說，一張貓的圖片在經過旋轉或鏡像後仍然應該被認為是一隻貓。我們說我們的編碼模型在這樣的情況下「對旋轉及鏡像變換具有等變性」。

註二：在實驗中，第一層係數映射只使用了一個Gabor filter作為字典的唯一特徵，且在第二層中並未把第三種映射畫出來。

撰文｜葉宸甫

參考資料

Shewmake, Christian, Nina Miolane, and Bruno Olshausen. 2023. “Group Equivariant Sparse Coding.” In Geometric Science of Information, edited by Frank Nielsen and Frédéric Barbaresco, 91–101. Lecture Notes in Computer Science. Cham: Springer Nature Switzerland. https://doi.org/10.1007/978-3-031-38271-0_10.