模擬神經之間的層級關係
我們知道在 neuron-level 的學習就是所謂的 synaptic plasticity,也就是神經之間的 synapse 連結,可以透過 LTP (long-term potentiation) 來增強、透過 LTD (long-term depression) 來減弱.偶爾一些 neuromodulator 像是 dopamine 也可以來進行一些場外指導,但只有 neuromodulator 顯然是不夠的,因為靠化學物質來影響神經需要一段時間.因此這篇 paper 想要問的就是,神經如何在 local 端透過’高層級’的訊號來控制’低層級’訊號的 synaptic plasticity ,也就是可以有一個指令告訴這顆神經的連結應該要增強還是減弱(圖一).
 |
| 圖一 |
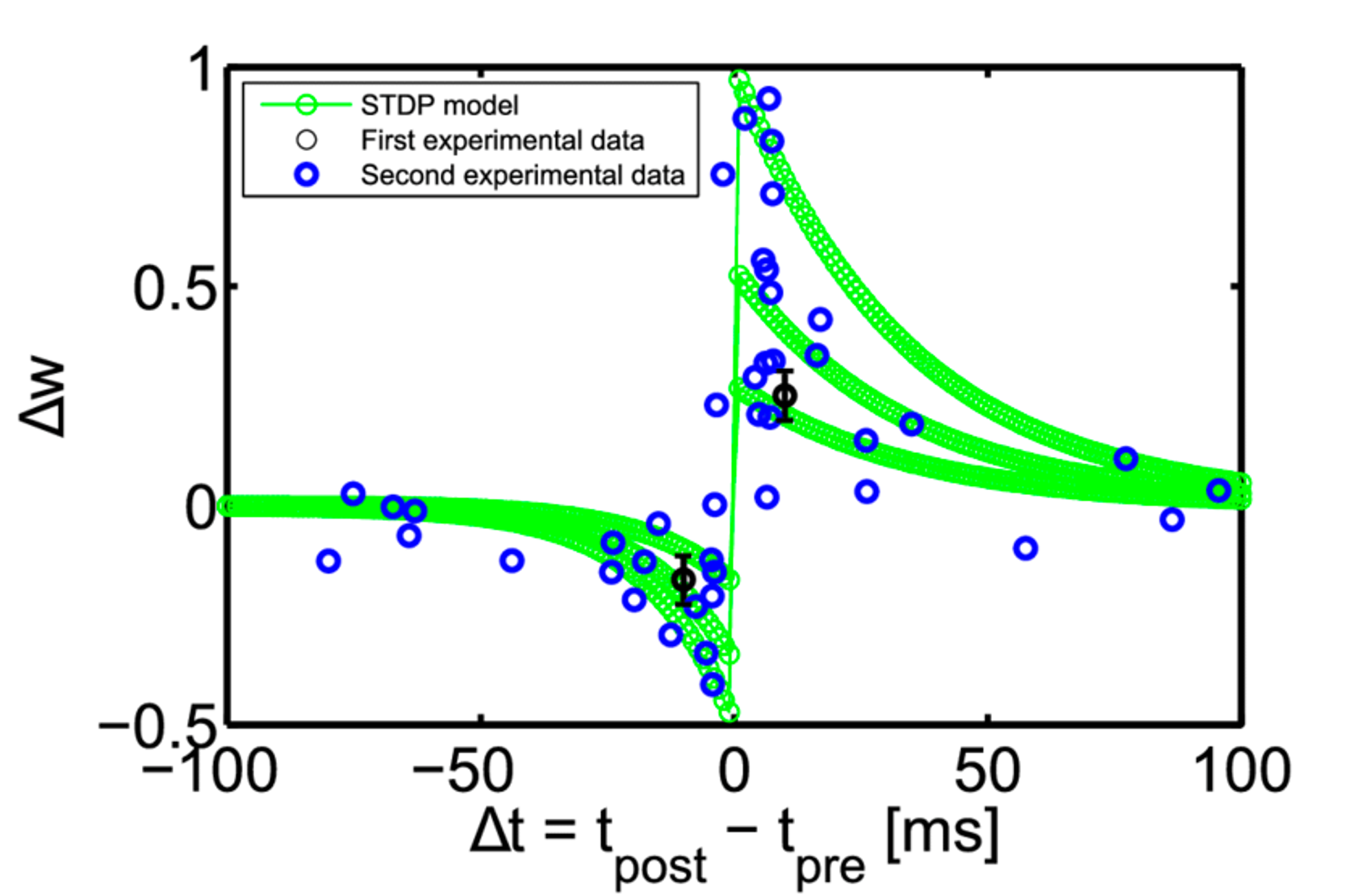
Synaptic plasticity 就是發生在 pre- 跟 postsynaptic neuron 之間的連結增強或減弱 weight change的過程(圖二).一般的 STDP (spike-timing-dependent plasticity) 模型,是根據 pre- 跟 post-synaptic spike 的時間差來決定會發生 LTP(增強) 還是 LTD (減弱) .如果 pre-synaptic spike 先於 post-synaptic spike 發生,時間差為正,那麼連結就會被增強 weight change 為正;反之如果 post-synaptic spike 先於 pre-synaptic spike 發生,時間差為負,那麼連結就會被減弱 weight change 為負(圖三).
 |
| 圖二 |
 |
| 圖三 |
此篇文章的模型與 STDP 模型不一樣,他是 Burst-dependent model,也就是根據 post-synaptic model 有沒有產生 “Burst” 來決定會不會進行連結增強.所謂 Burst 就是指有兩個以上的 spike 接連發生.如果有 Burst 發生,那連結 synapse 就會增強;反之如果沒有 Burst 發生,那連結 synapse 就會減弱(圖四).值得注意的是,在他的計算公式中還有加入 P_bar 這一項,代表的是神經的過往經歷中 Burst 發生的機率.如果 P_bar 很高,在發生減弱(沒有 burst)的時候,減弱的程度會被提升,而發生增強(有 burst)的時候,增強的程度會被下降,以此來調控神經連結的強度.因此,在圖五我們可以看到,在 pre- 跟 post-neuron 都是隨機活動的情況下,x 軸代表的是隨機活動的頻率,y 軸代表的是 weight change ,而我們要觀察 weight change 從負變到正的情形.給予不同的 P_bar 值,我們會發現他們 weight change 的變化情形是不一樣的,也就是這顆神經過往的 Burst 歷史會影響他之後的 plasticity 情形.
 |
| 圖四 |
 |
| 圖五 |
那究竟是什麼東西影響神經到底有沒有 burst 呢?在這個模型中,他們設定是 distal,也就是離 soma 比較遠的部分的 dendrite 的輸入,會影響這顆神經會不會有 burst .如圖六,當 distal 有強的輸入 (strong distal),神經的 Burst 機率就會增加(e圖的紅色線),最終會產生正的 weight change(f圖).反之,當distal 有弱的輸入 (weak distal) ,神經的 Burst 機率就會減少(e 圖的紅色線),最終會產生負的 weight change(f 圖)。
 |
| 圖六 |
圖七的模型當中,有兩群 neurons ,分別接受低層級資訊 I_s 以及高層級資訊 I_d ,而這張圖的結論想要告訴我們的是,他們的模型能夠在兩群神經互相連結互相傳輸訊號的情況下,仍然保留 I_s 與 I_d 訊號的內容,而不會被掩蓋掉,這也就是他們研究神經層級關係的模型的目的.
 |
| 圖七 |
再後面這篇文章還有提到用他們建構的模型所做的一些學習效果,有興趣的讀者可以移步閱覽.(Payeur et al 2021)
撰稿人:周品汝
Reference:
Payeur, Alexandre, et al. "Burst-dependent synaptic plasticity can coordinate learning in hierarchical circuits." Nature neuroscience 24.7 (2021): 1010-1019.
ScienceFacts.net
Azghadi, M. R. (2014). Neuromorphic VLSI designs for spike timing and rate-based synaptic plasticity with application in pattern classification (Doctoral dissertation, Ph. D. dissertation, The University of Adelaide, Adelaide, Australia, http://hdl.handle.net/2440/84732).


留言
張貼留言