神經網路的雙穩態切換

https://mire-growth-131.notion.site/5bf2d626e1a047edaaf80bb158486e33

雙穩態(Bistable)指系統存在兩個穩態，高穩態和低穩態。在大腦的觀測當中能發現皮層在沒有外部刺激的情況下能持續活躍。這種現象可能對工作記憶和注意力至關重要。因此 Klaus Obermayer 教授的研究團隊透過模擬，了解神經網路如何再用最有效率的刺激下再兩個穩態切換。

神經模型

模型含有兩群神經，分別代表興奮性與抑制性 (圖1)，分別受到背景刺激與時變刺激。利用梯度下降法 (Gradient descent) 去更新給模型的刺激。就像在山谷間找到最快的下滑路徑。而作者的損失函數 (loss function)包含三項，其中 Sparsity cost 用來看對哪群神經刺激比較有效率 (L1 constrain)；而 Energy cost 用來尋找最小的刺激振幅 (L2 constrain)。

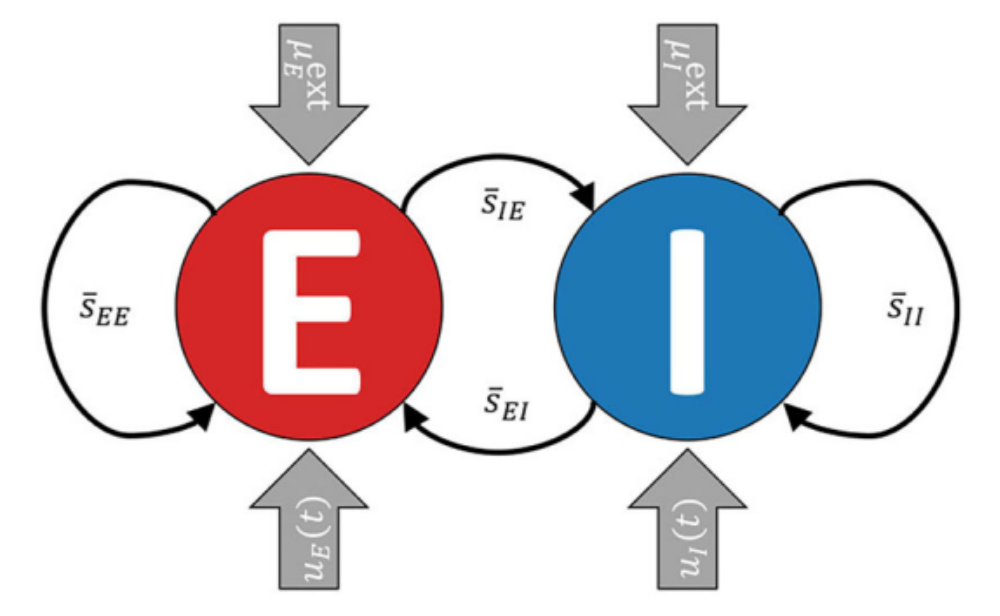圖1. 神經模型示意圖

訓練結果

透過訓練能發現雙穩態的最小刺激 (圖2)。down→up 表示低穩態到高穩態；L1與L2表示損失函數的兩種限制。第一列表示兩群神經的變化，第二列則表示刺激的大小。

圖2. 模型的訓練結果

結論

作者透過簡化的兩群模型，找到網路如何能最有效率的切換，讓我們能更了解神經網路如何運作。

撰文：謝明儒

參考資料

Salfenmoser, L., & Obermayer, K. (2022). Nonlinear optimal control of a mean-field model of neural population dynamics. Frontiers in computational neuroscience, 1.