A Worked Example of Linearizing a Nonlinear Ordinary Differential Equation: Predator-Prey System with Refuge

$\newcommand{\la}{\lambda}$

$\DeclareMathOperator{\tr}{tr}$

I have talked before about how to analyze a nonlinear system with the linearization technique. I wanted to give an example that I had for homework in my graduate ordinary differential equations class. Hopefully this will help show the steps one goes through when presented with a nonlinear systems.

we are asked to analyzes the predator prey system with refuge. There is some prey animal species $x$ that is eaten by a predator $y$.

$$x' = ax -c_1 y (x-k)$$
$$y' = -e y + c_2 y (x-k)$$
here all terms are positive, that is $a,c_1,c_2,e,k>0$.
There is always a source of prey, thus the term $ax$ The Predators must eat the prey. If they do not eat enough, they die off. Thus the term $-ey$. Predation is captured by the term $y(x-k)$. Here there is a refuge term $k$  (there is some refuge they have where the predator cannot hunt them).

To begin analysing the system we begin by calculating the equilibrium points. This system has equilibrium points $(0,0)$ and $(\frac{e+c_2 k}{c_2},\frac{a(e+c_2 k)}{c_1 e})$.


This can easily be seen by solving the above two equations

$$0 = ax -c_1 y (x-k)$$
$$0 = -e y + c_2 y (x-k)$$
Some basic algebra shows
$$0 = -e + c_2 (x-k)$$
$$\frac{e +c_2 k}{c_2}  = x$$
We can then use this to solve $y$ as
$$0 = a\frac{e +c_2 k}{c_2} -c_1 y (\frac{e +c_2 k}{c_2}-k)$$
$$0 = a(e +c_2 k)-c_1 y (e +c_2 k-k c_2)$$
$$0 = a(e +c_2 k) -c_1 y (e)$$
yields
$$y= \frac{a(e+c_2 k)}{c_1 e}$$ after some simplification.

The next step is to compute the stability of the fixed points.
In general the system has the Jacobian matrix
$$\begin{pmatrix} a - c_1 y & c_1 x + c_1 k \\ c_2 y & -e -c_2 k + c_2 x \end{pmatrix}$$

For the point $(0,0)$ we have the Jacobian matrix
$$\begin{pmatrix} a & c_1 k \\ 0 & -e -c_2 k \end{pmatrix}$$
This is an upper triangular matrix. As such its eigenvalues are $\lambda=a, -e -c_2 k$. Note here all parameters are positive. Therefore this has one positive eigenvalue $a$ and one negative eigenvalue $-e-c_2 k$. Thus $(0,0)$ is a saddle equilibrium.


Next we compute the eigenvalues at the other equilibrium point.

$$\begin{pmatrix} a - c_1 y & c_1 x + c_1 k \\ c_2 y & -e -c_2 k + c_2 x \end{pmatrix}$$

The eigenvalues of the above "general" matrix are $\la = \frac{1}{2}(-\tr\pm\sqrt{\tr^2-4\det})$
an obtuse amount of plugging and chugging yields the following formula
$$\frac{1}{2}(a -e -c_2 k + c_2 x -c_1 y \pm \sqrt{((a -e -c_2 k + c_2 x -c_1 y )-4(-ae -ac_2k+ac_2x +c_1ey)})$$
Plugging in our eq point for $x$ and $y$ gives us the easier eigenvalues.
$$\la = \frac{-a c_2 k \pm e\sqrt{-4 a(e+c_2 k)+ \frac{a^2 c_2^2 k^2}{e^2} } }{2e}$$
Lets begin with two simple observations about the radical. Because $e>0$ and $c_2 k>0$ We know that $$-a c_2 k>\sqrt{-4 a(e+c_2 k)+ \frac{a^2 c_2^2 k^2}{e^2} }$$ .Therefor no matter what the values of the parameters both eigenvalues will be less than zero. Therefor the equilibrium point $(\frac{e+c_2 k}{c_2},\frac{a(e+c_2 k)}{c_1 e})$ is always stable.

Moreover if the part under the radical satisfies the inequality
$$e^2 (4ae +4 c_2 k) > a^2 c_2^2 k^2$$

Then the eigenvalues will be a conjugate imaginary pair with negative real part. This gives us a spiral sink at the equilibrium. If it is less than this critical value then it is a stable node. At exactly $e^2 (4ae +4 c_2 k) = a^2 c_2^2 k^2$
 we have a improper stable node.
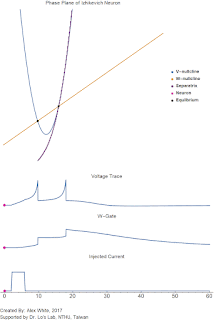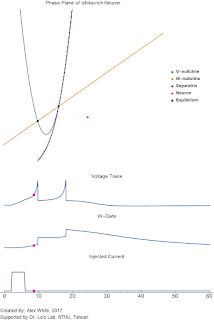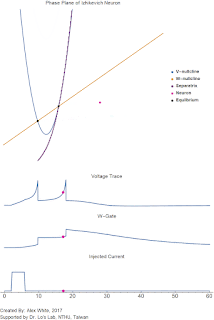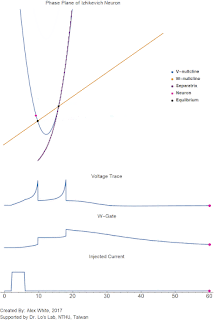
Below I have computed an example with fixed parameters except for $e$. As $e$ varies there is a point where non-oscillatory dynamics become oscillatory.

Hopefully this worked example can help you see the steps one goes through when analyzing a nonlinear system.

The phase plane of the system with varying $e$ from 1 to 15. The parameters are $a=3$, $c_1 =c_2= 1$, and $k = 10$. Notice how the stable equilibrium changes from a stable sink to a stable spiral. 

Author: Alexander White