Izhikevich's Simple Neurons: Part One
中文在這裡
The Izhikevich model neuron is a relatively recent addition to the many neuron models used in computational neuroscience. It was created by Dr. Izhikevich in 2003, and is one of the simplest nonlinear models of a neuron. For Part One of this series, I want to give a brief introduction to his model, and build up a intuition of how the model works. Over the next few posts I will give increasingly in-depth analysis of the model, and eventually walk through each step of how to construct various versions of the model.
The Izhikevich neuron is an integrate-and-fire type neuron, which means that it does not explicitly model the repolarizing downswing of an action potential (or spike). It approximates the downswing with a voltage discontinuity, resetting the voltage to a new value after voltage has surpassed a certain threshold. Despite this simplicity, Izhikevich neurons are highly flexible and can capture many of the rich computational properties of single neurons. Yet, they are also very easy to simulate efficiently, making an excellent choice for networks with more than one neuron.
Many neural network papers, especially papers focusing on performing some task, usually simplify the individual neurons in the network they are studying. There are many different levels of simplification. The simplest are firing rate models that do not even attempt to model action potentials. Examples like the perceptron are quite common in artificial neural networks(ANN). The simplest model that can capture spiking dynamics is the linear leaky integrate-and-fire (LIF) model, which is capable of modeling when action potentials occur. However the LIF model fails to capture the rich repertoire of possible computations that many individual neurons can perform.
 |
| Figure 1: Original version of Izhikevich model with a sampling of the
many computational subtypes. Thanks to Dr. Izhikevich, the electronic
version of the figure and reproduction permissions are freely available
at http://www.izhikevich.org/publications/spikes.htm |
Enter the Izhikevich neuron model. Because of the simple quadratic non-linearity in voltage, it is able to better model action potential generation than the LIF model, and thus is able to capture many of the possible computational properties of single neurons. However, the model is still very easy to simulate, and thus is perfect for simulations of networks that require more biological plausibility than the LIF can offer, and still run in a reasonable amount of time.
Before any computational neuroscientist builds a neural network, they take time understand how the individual neurons in the network function. With that in mind, we will walk through the intuition of a single Izhikevich neuron's spikes. This will lay the groundwork for my next few blog articles when we talk about the vast repertoire of other possible Izhikevich neurons that can be created with the same underlying equations.
Lets jump right in and begin by defining the unitless (no reference to millisecond or millivolt scales) version of the Izhikevich model:
$$ \frac{dV}{dt} = V^2 - W + I $$
$$ \frac{dW}{dt} = a (b V - W)$$
$$ V > V_{spike}, V\rightarrow c, W \rightarrow W+d$$
 |
| Figure 2: A sample spike from the model presented in figure 1. The
parameters a, b, c, and d all represent the same properties regardless
of the version of the model. |
The equation has two state variables. The first state variable is $V$ which plays the part of membrane voltage of a neuron. The variable $W$ plays the role of a linearized potassium current . The simple nonlinear term is $V^2$ and it represents the sodium current. If the voltage ever exceeds $V > V_{spike}$ we say the neuron has fired an action potential, or has "spiked". Often this value roughly corresponds to the peak voltage during the action potential and thus is often set around $+50$ $mV$. When $V> V_{spike}$ then we reset voltage to $c$ (often around $-60$) and the $W$ gate is increased by a amount $d$. Here, $d$ models the effect of the action potential's downswing of the potassium like $W$ gate.
Notice how we said that $V^2$ represents "sodium" and $W$ represents "potassium". That's because these terms approximate the biological function of these ions in real neurons. In this model $V^2$ is responsible for the action potentials depolarizing upswing, just like sodium current is responsible in biological neurons. While we don't explicitly model the repolarizing downswing of the action potential, instead we just reset voltage to the a hyperpolarized value $c$ and add $d$ to $W$-gate, to simulate to opening of the potassium channels during the spike's downswing. $W$ helps control the refractory period of the model neuron. The more positive $W$, the less likely the neuron model is to fire. Thus $W$ allows us to more accurately reflect the effect of ion channels on refractory periods after action potentials.
A reader with more biological background may be thinking about the inactivation gates in sodium channels, as they are also responsible for the refractory period, so in a way the $W$-gate represents both the sodium inactivation, and potassium activation. This simplification all relies on two highly related topics manifold reduction and, topological equivalence. These are the mathematical tools we use to estimate the physical process underlying action potential generation, and maintain the qualitative aspects to keep the resulting dynamics and thus computational properties the same. For more in depth understanding read chapter of 8 Dr. Izhikevich's book, but for now the main take away is we model action potential depolarizing upswing with $V^2$, action potential repolarizing downswing with $d$, and refractory period dynamics with $W$, and these there variables will be sufficient to capture a wide array of possible neural computations.
What do the parameters $a$ and $b$ represent? To answer that question in depth we will add more parameters, but essentially they are the parameters that dictate how quickly the $W$-gate decays towards zero, at any given voltage $V$. Next, let's consider the more biologically realistic Izhikevich neuron model
$$ C_m \frac{dV}{dt} = k (V-V_r)(V-V_{th}) - W + I $$
$$ \frac{dW}{dt} = a(b(V-V_r) - W)$$
$$ V > V_{spike}, V\rightarrow V_{reset}, W \rightarrow W+d$$
These extra parameters rescale time and voltage and give the equations physical units like milliseconds or millivolts. In these new equations we have added the parameters $C_m$ which is like a capacitance, $k$ which is like the conductance of the sodium channel, $V_r$ which is the rest potential of the neuron, and $V_{th}$ which is an estimate neurons voltage threshold. Now, the parameter $a$ represents the time constant for the $W$ gate. It's value dictates how quickly the $w$ gate exponentially decays to rest. Likewise, $b$ represents how much voltage $V$ influences $W$'s decay. In our case $b$ will be small, but as we will see in later blog posts that large values of $b$ will play a role in some interesting versions of the model.
The amazing thing, about the these two sets of equations is they can be rescaled and transformed into one another by a coordinate transform. If one rescales $V$, $W$, $I$, and $t$ then the equation reduces to the unitless form. This rescaling does not change the dynamic or computational properties of the neurons. In fact we require that this transform does not change the dynamics, and the two systems remain topologically equivalent. Note that the parameters $a$ and $b$ are still present in both sets of equations, even thought there numerical values may be different. This reflects the fact that parameters are required to maintain the computational properties of the system, and cannot be rescaled away. Why would we want to rescale between the sets of equations? Sometimes working in one coordinate system is easier than the other, much like working in a different coordinate system in physics makes the math easier. The main takeaway here is the important properties of spike dynamics remain constant under this coordinate transform.
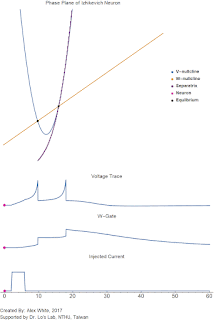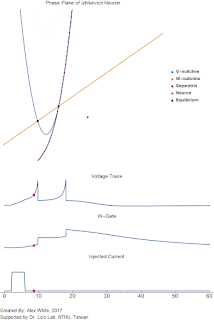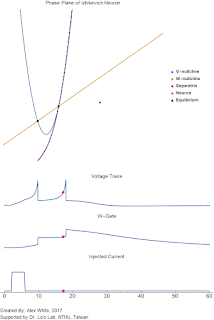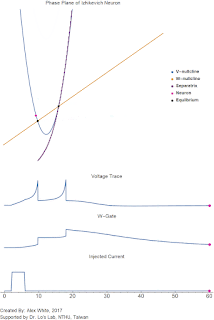
Now lets discuss the dynamics. As always, we start with looking at the nullclines and the equilibrium points in the phase plane. Recall that the $V$-nullcline is the curve where $\frac{dV}{dt}=0=V^2 - u + I$ and is the blue quadratic curve in the GIF. Likewise, the $W$-nullcline is the yellow line where $\frac{dW}{dt}= 0 = a(b V - W)$. Notice when $I = 0$ there the nullclines intersect in two places. These are the two equilibrium points. Recall that if an initial condition starts on equilibrium point it stays on the equilibrium point unless pushed away from by an injected current $I$.
For our system, the left most one is a stable rest equilibrium. Because the left equilibrium point is stable, that means any initial condition that starts near it will slowly decay back to rest. The second equilibrium is a saddle point. Thus it is unstable in the horizontal direction, and stable in the vertical direction. This saddle splits the phase plain into two parts, divided by the zig-zaggy purple line called the separatrix. the left hand side of the separatrix all initial conditions go to the rest equilibrium, and the neuron does not fire. However, on the right side of the separatrix all solutions explode towards $+\infty$. One can think of the separatrix as the threshold of the neuron. If for some reason we landed perfectly on the separatrix, we would slowly decay towards the rightmost equilibrium. This is what we mean by a saddle point.
How do we know the left equilibrium was stable and the right equilibrium was a saddle. One can use linearization and look at the eigenvalues of the resulting Jacobian matrix. The stable equilibrium has two eigenvalues with negative real part, and the saddle point has one negative eigenvalue and one positive eigenvalue.In the next blog article I will discuss in depth how to perform the linearization, but if you are unfamiliar with eigenvalues and linearization I suggest looking into it here. As an exercise, try to show that the left equilibrium is always stable in the biologically realistic system. Assume $a, k, C_m>0$, and $V_{th}, b< 0$. When $b>0$ the left equilibrium is *almost* always stable. When is it unstable? I'll show the answer next blog.
In the GIF, when we briefly inject a positive current $I$ into our neuron for 4 milliseconds, it causes our blue nullcline to move upward until there are no equilibrium points. Because there are no equilibrium points the voltage begins to rise (our pink dot). Our pink dot begins to accelerate, moving faster and faster towards positive infinity. Then, when our current turns off, the two equilibrium points return. But it is too late, the solution has already passed the separatrix. The pink dot continues to accelerate towards infinity, and the neuron fires a spike.
Note, However that the neuron voltage does not actually explode to $+\infty$, we catch it at $V_{spike}$, and then we reset the voltage to $c$ and increase the $W$-gate by $d$. one can imagine that the solution goes outside the plotted region, loops back and then returns to a new location in our plotted region. This is approximating the downswing of the action potential. Notice that simulated neuron will spike twice because after the first spike we reset to a location on the right side of the separatrix. Therefore the solution will again explode to infinity. However, after the second spike the recovery variable $W$ is much more positive (it has had $d$ added twice to it now). Thus our pink dot is reset to the left of the separatrix. Thus, after some time our neuron will return to rest and stop firing.
This is the essence of the spiking mechanism behind the Izhikevich model. We haven't even begun to explain the many different types of computational properties that this system is capable of, nor have we gone into the details of analyzing the equilibrium points. Next article I will discuss the dynamics of the rest equilibrium, and show a Izhikevich model capable of resonance, a behavior impossible in LIF neurons.
Author: Alexander J. White
Source: http://www.izhikevich.org/publications/spikes.htm



留言
張貼留言