分類神經形態的新指標

神經形態對於功能至關重要，而拓撲學（Topology）是一個有助於研究神經型態的方法，可以評估神經元網絡的複雜性、連接密度以及不同區域之間的關聯性，有助於深入理解神經系統的結構和功能。作者提出Tip-support distribution的概念以定量、描述神經形態。

Tip-support distribution的關鍵特點在於對數圖會遵循冪次法則（Power-law distribution），其斜率為-α，並且透過β= |α| /2計算與定義完美指數（Perfection index，β），以果蠅幼蟲神經（β=0.7）為例，介於完美二元樹（Perfect Binary Tree，β=1）與最不完美樹（Maximally Imperfect Tree，β=0）之間（Fig1）。

Fig1. 果蠅幼蟲第四類感覺神經（class IV neurons）的Tip-support distribution遵循冪次法則（Power law），M (n )~$n^{-α}$。(A) 果蠅幼蟲的第四類感覺神經透過GPF成像。(B) 第四類感覺神經上半部分的樹狀圖。(C) 不同背側的第四類感覺神經斜率α：-1.40 ± 0.04（α=0：最不完美樹、α=-2：完美二元樹）。(原文Figure 1)

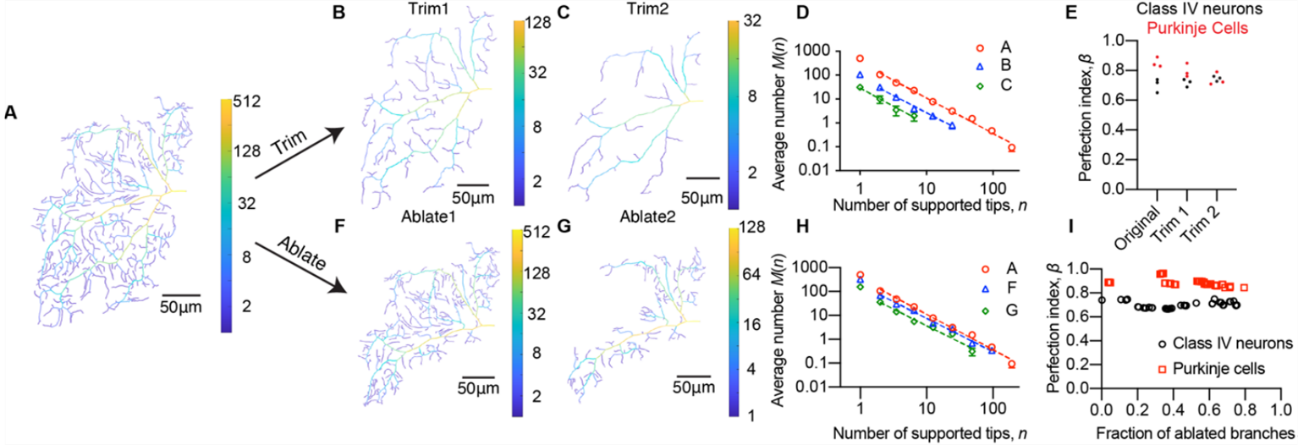
研究還發現將同一種神經修剪後，Tip-support distribution仍會遵循冪次法則，完美指數也保持不變，這表明神經元的生長過程存在共同的分支規則（Fig2）。這個結果說明了即使樹的不對稱性（Tree asymmetry）在區分不同類型的神經形態就表現得相當出色，然而新提出的Tip-support distribution不僅可以區分不同類型的神經形態，還提供了對神經元生長機制的理解，這對於深入研究神經系統的結構和功能非常有價值。

Fig2. 隨機去除部分的分支不會影響完美指數。(A) 部份的第四類感覺神經。(B) 第一次去除末端分支。(C) 第二次去除末端分支。(D) $α_{A}$=−1.48、$α_{B}$=−1.45、$α_{C}$=−1.52。(E) 第四類感覺神經和浦肯野細胞在修剪前、修剪第一次與修剪第二次的完美指數。(F) 第一次去除內部分支（修剪35%）。(G) 第二次去除內部分支（修剪69%）。(H) $α_{A}$=−1.48、$α_{F}$=−1.39、$α_{G}$=−1.38。(I) 神經元和浦肯野細胞的完美指數。(原文Figure 3)

撰文：余旻珊

參考文獻：

Maijia Liao, Alex D. Bird, Hermann Cuntz, Jonathon Howard. Topology recapitulates ontogeny of dendritic arbors. https://doi.org/10.1101/2023.02.27.530331